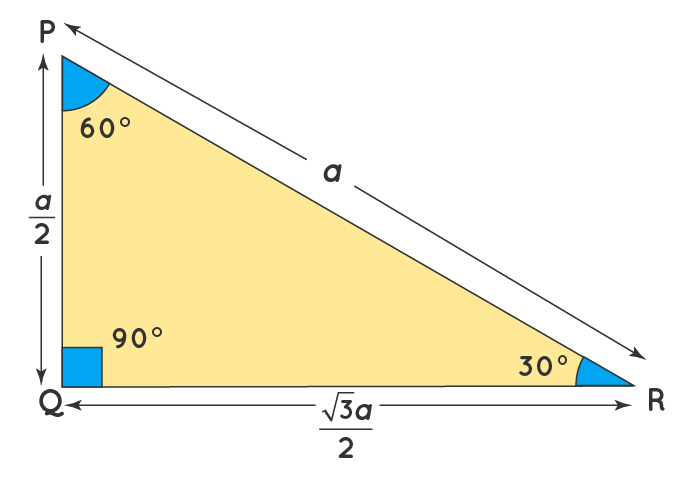
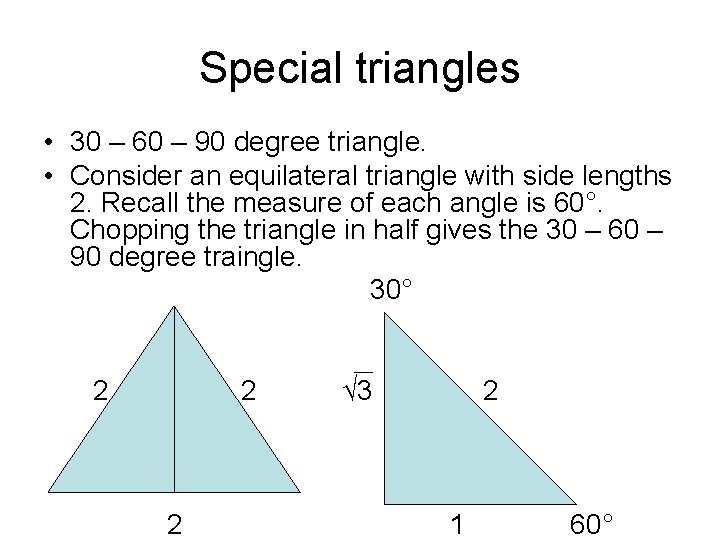
This means that the ratio of the lengths of the shortest side to the hypotenuse of any right triangle is 12 Therefore, If a triangle is a right triangle, the ratio of the sides (short leglong leghypotenuse) is 1√32A triangle is a special right triangle whose angles are 30º, 60º, and 90º The triangle is special because its side lengths are always in the ratio of 1 √32 Any triangle of the form can be solved without applying longstep methods such as the Pythagorean Theorem and trigonometric functionsSpecial Right Triangles in Geometry and

30 60 90 Triangle Theorem Ratio Formula Video
What are the sides of a 30 60 90 triangle
What are the sides of a 30 60 90 triangle-A triangle is a special right triangle with some very special characteristics If you have a degree triangle, you can find a missing side length without using the Pythagorean theorem!It is based on bisecting an equilateral triangle and using the Pythagorean theorem A 30°60°90° triangle is formed when an equilateral triangle is bisected This makes the Hypotenuse a
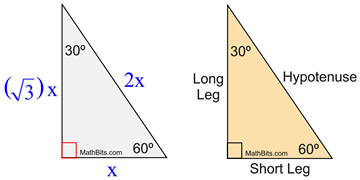



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math
Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another The basic triangle ratio is Side opposite the 30° angle x Side opposite the 60° angle x * √ 3 Side opposite the 90° angle 2 xFor example, a degree triangle could have side lengths of2, 2√3, 47, 7√3, 14√3, 3, 2√3 We can see that this is a right triangle in which the hypotenuse is twice the length of one of the legsMore items•The 30 – 60 – 90 degree triangle is in the shape of half an equilateral triangle, cut straight down the middle along its altitude It has angles of 30°, 60°, and 90° and sides in the ratio of The following figure shows an example Get acquainted with this triangle by doing a couple of problems
A triangle is a unique right triangle that contains interior angles of 30, 60, and also 90 degrees When we identify a triangular to be a 30 60 90 triangular, the values of all angles and also sides can be swiftly determined Imagine reducing an equilateral triangle vertically, right down the middleCheck out this tutorial to A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degreesBecause it is a special triangle, it also has side length values which are always in a consistent relationship with one another
Answer (1 of 5) Why in a triangle is the the side opposite 60 degrees x (sqrt(3))? The 30 60 90 triangle is special because it forms an equilateral triangle when a mirror image of itself is drawn, meaning all sides are equal!The property is that the lengths of the sides of a triangle are in the ratio 12√3 Thus if you know that the side opposite the 60 degree angle measures 5 inches then then this is √3 times as long as the side opposite the 30 degree so the side



1




30 60 90 Triangle Calculator Formula Rules
This page shows to construct (draw) a 30 60 90 degree triangle with compass and straightedge or ruler We are given a line segment to start, which will become the hypotenuse of a right triangle It works by combining two other constructions A 30 degree angle, and a 60 degree angleBecause the interior angles of a triangle always add to 180 degrees, the third angle must Hence the three sides of the 30°60°90° triangle are c/2, √3c/2 & c where c is the hypotenuse The basic triangle ratio is Side opposite the 30° angle x Side opposite the 60° angle x * √3 Side opposite the 90° angle 2x All degree triangles have sides with the same basic ratio Two of the most common right triangles are and degree triangles If you look at the 30–60–90degree triangle in radians, it translates to the
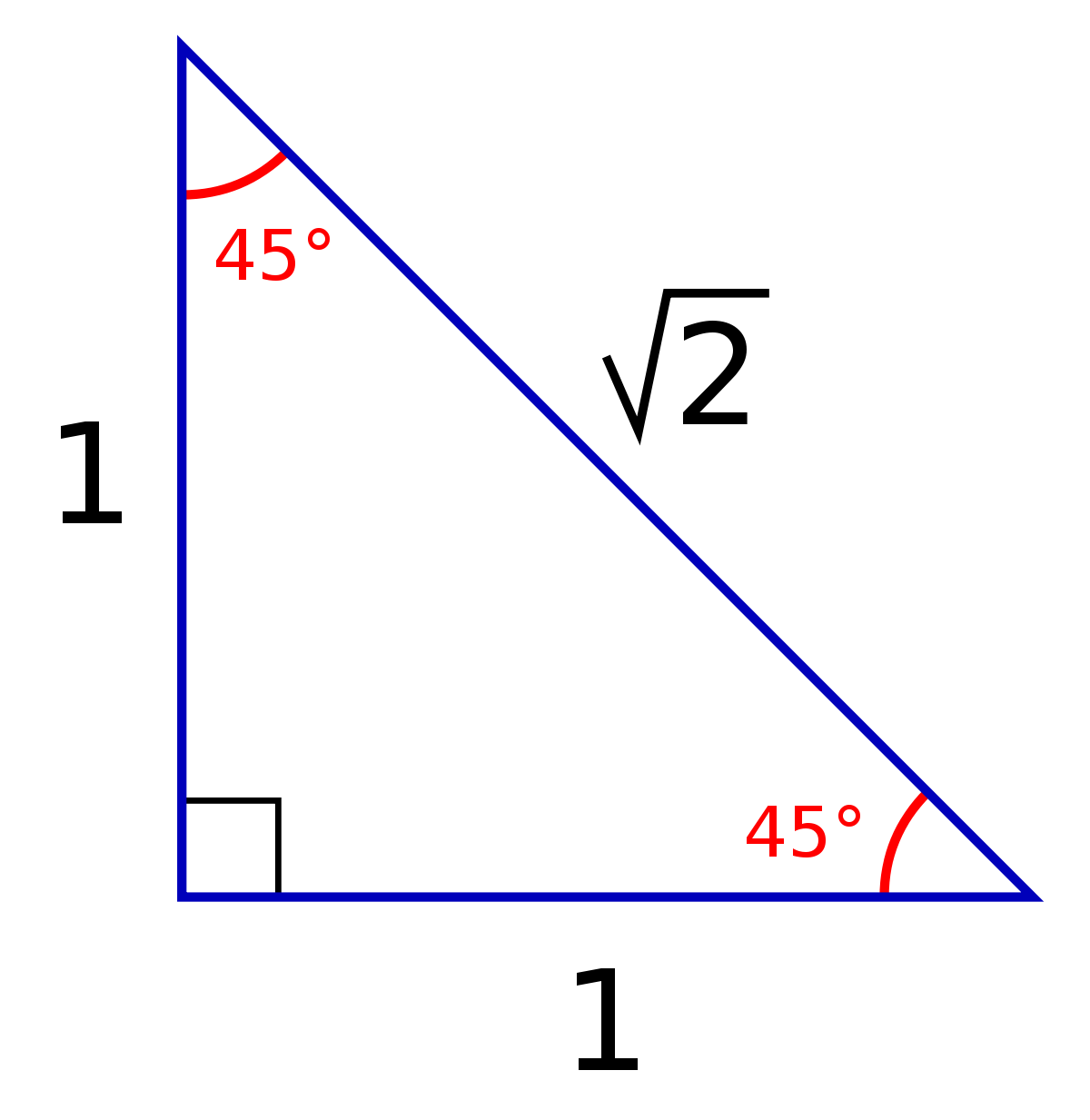



File 45 45 Triangle Svg Wikimedia Commons



1
The property is that the lengths of the sides of a triangle are in the ratio 12√3 Thus if you know that the side opposite the 60 degree angle measures 5 inches then then this is √3 times as long as the side opposite the 30 degree so the sideA triangle is a special right triangle with some very special characteristics If you have a degree triangle, you can find a missing side length without using the Pythagorean theorem! 30 60 90 triangle sides If we know the shorter leg length a, we can find out that b = a√3 c = 2a If the longer leg length b is the one parameter given, then a = b√3/3 c = 2b√3/3 For hypotenuse c known, the legs formulas look as follows a = c/2 b = c√3/2 Or simply type your given values and the 30 60 90 triangle calculator will do the rest!




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




30 60 90 Triangle Theorem Ratio Formula Video
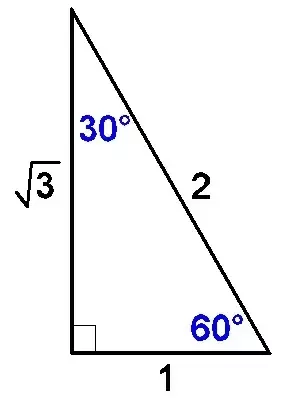
Triangle in trigonometry In the study of trigonometry, the triangle is considered a special triangleKnowing the ratio of the sides of a triangle allows us to find the exact values of the three trigonometric functions sine, cosine, and tangent for the angles 30° and 60° For example, sin(30°), read as the sine of 30 degrees, is the ratio of the sideFind the remaining sides of a triangle if the opposite side of 60 degrees is 6 Right Triangle and Trigonometric Ratios A triangle with one right angle is called a30°60°90° Triangles There is a special relationship among the measures of the sides of a 30 ° − 60 ° − 90 ° triangle A 30 ° − 60 ° − 90 ° triangle is commonly encountered right triangle whose sides are in the proportion 1 3 2 The measures of the sides are x, x 3, and 2 x



1




60x90 Degree Angle Triangle Google Search Picture For You Math Apps Math Formulas Studying Math
A triangle is a right triangle with angle measures of 30º, 60º, and 90º (the right angle) Because the angles are always in that ratio, the sides are also always in the same ratio to each other The side opposite the 30º angle is the shortest and the length of it is usually labeled as x The side opposite the 60º angle has aAll triangles, have sides with the same basic ratio If you look at the degree triangle in radians, it translates to the following 30, 60, and 90 degrees expressed in radians The figure illustrates the ratio of the sides for the degree triangle A degree right triangle A degree right triangle A 30–60–90 triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degreesBecause it is a special triangle, it also has side length values which are always in a consistent relationship with one another
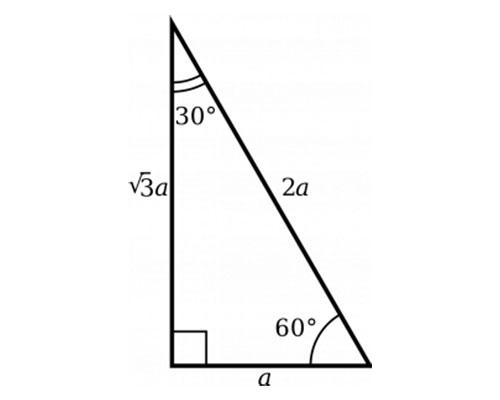



30 60 90 Triangle Sides Examples Angles Full Lesson
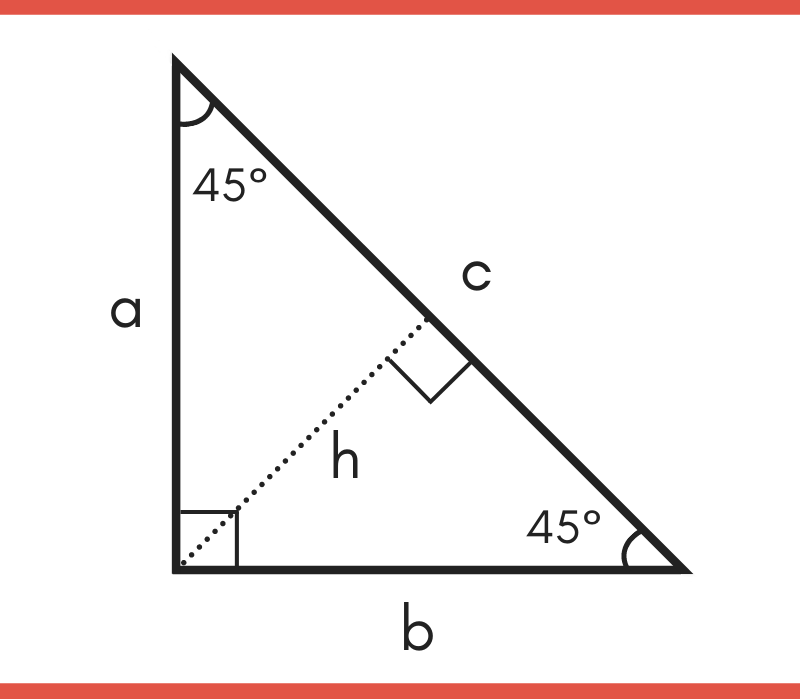



45 45 90 Special Right Triangle Calculator Inch Calculator
A 30 60 90 triangle is a special type of right triangle What is special about 30 60 90 triangles is that the sides of the 30 60 90 triangle always have the same ratio Therefore, if we are given one side we are able to easily find the other sides using the ratio of 12square root of three A triangle has sides that lie in a ratio 1√32 Knowing these ratios makes it easy to compute the values of the trig functions for angles of 30 degrees (π/6) and 60 degrees (π/3) SpecificallyRight triangle calculator, 30 60 90 formula, 45 triangle, special area, unit circle calculator




Solved Special Right Triangles 30 Degree 60 Degree 90 Chegg Com



Right Triangles Gmat Free
Let's move on to solving right triangles with our knowledge on the sides' ratios Solve for 30 60 90 triangle Here we have a special right triangle, with the three interior angles of 30, 60, 90 degrees We know that the length of each side in this triangle is in a fixed ratio We can now use the ratio to solve the following problem30 60 90 Triangle Ratio A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one anotherIn a triangle, the ratio of the sides is always in the ratio of 1√3 2 This is also known as the triangle formula for sides yy√32y Let us learn the derivation of this ratio in the triangle proof section Consider some of the examples of a degree triangle with these side lengths



The Easy Guide To The 30 60 90 Triangle




Special Right Triangle Wikipedia
A special right triangle is a right triangle having angles of 30, 60, 90, or 45, 45, 90 Knowledge of the ratio o About Press Copyright Contact usA right triangle (literally pronounced "thirty sixty ninety") is a special type of right triangle where the three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant because the sides exist in an easytoremember ratio 1 √3 3 2Therefore in a 30°60°90° triangle the sides are in the ratio 1 2 ;




Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation
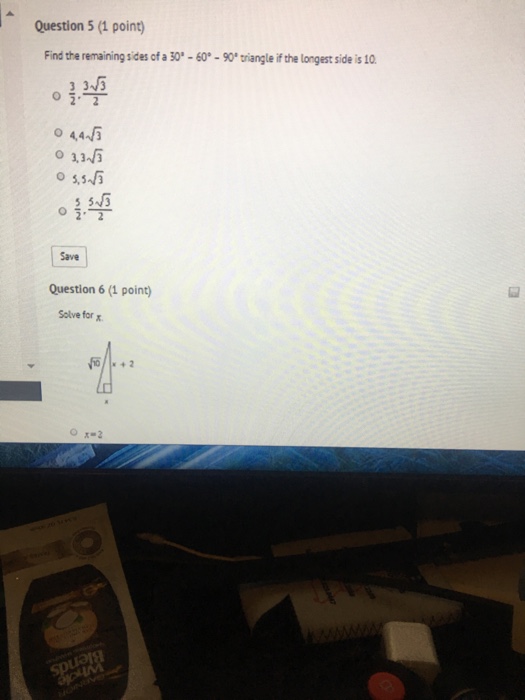



Solved Find The Remaining Sides Of A 30 Degree 60 Degree Chegg Com
Segment AF is therefore the long leg of this triangle, with a length of √3 AF, length √3, and FC, the short leg of the triangle, together form dodecagon radius AC, already set at length 2 By length subtraction, then, FC, the triangle's short leg, has a length of 2 – √3A theorem in Geometry is well known The theorem states that, in a right triangle, the side opposite to 30 degree angle is half of the hypotenuse I have a proof that uses construction of equilateral triangle Is the simpler alternative proof possible using school level Geometry I want to give illustration in class roomTriangles are classified as "special right triangles" They are special because of special relationships among the triangle legs that allow one to easily arrive at the length of the sides with exact answers instead of decimal approximations when using trig functions
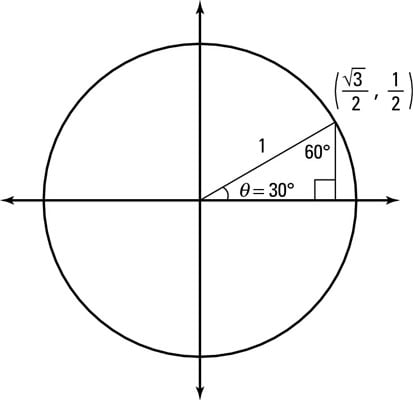



How To Plot The Major Angles Of The Whole Unit Circle Dummies



The Easy Guide To The 30 60 90 Triangle
The triangle is one example of a special right triangle It is right triangle whose angles are 30°, 60° and 90° The lengths of the sides of a triangle are in the ratio of 1√32 The following diagram shows a triangle and the ratio of the sides Scroll down the page for more examples and solutions on how to useWhat is a Degree Triangle? We can see, therefore, that the side lengths for a triangle will always have consistent side lengths of x, x√3, and 2x (or $x/2, √3x/2$, and x) Luckily for us, we can prove triangle rules true without all ofthis When to Use Triangle Rules



Right Triangles Gmat Free
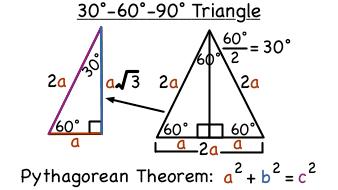



What Is A 30 60 90 Degree Triangle Virtual Nerd
The side lengths of a 30°–60°–90° triangle This is a triangle whose three angles are in the ratio 1 2 3 and respectively measure 30° ( π / 6 ), 60° ( π / 3The ratio of the sides follow the triangle ratio 1 2 √3 1 2 3 Short side (opposite the 30 30 degree angle) = x x Hypotenuse (opposite the 90 90 degree angle) = 2x 2 x Long side (opposite the 60 60 degree angle) = x√3 x 3A triangle is a special right triangle that contains internal angles of 30, 60, and 90 degrees Once we identify a triangle to be a 30 60 90 triangle, the values of all angles and sides can be quickly identified Imagine cutting an equilateral triangle vertically, right down the middle Each half has now become a 30 60 90 triangle




30 60 90 Triangles Special Right Triangle Trigonometry Youtube




30 60 90 Triangle Definition Theorem Formula Examples
If a triangle has angles of 30, 60 and 90 degrees it is called one of the SPECIAL TRIANGLES It is used extensively in mathematics because we can find EXACT answers for sine, cosine and tangent of the angles 30 and 60 degrees All the following triangles have angles ofIn this type of right triangle, the sides corresponding to the angles 30°60°90° follow a ratio of 1√ 3 2 Thus, in this type of triangle, if the length of one side and the side's corresponding angle is known, the length of the other sides can be determined using the above ratioMultiply this answer by the square root of 3 to find the long leg Type 3 You know the long leg (the side across from the 60degree angle) Divide this side by the square root of 3 to find the short side Double that figure to find the hypotenuse Finding the other sides of a triangle when you know the hypotenuse




30 60 90 Triangle Calculator Formula Rules



Why In A 30 60 90 Triangle Is The The Side Opposite 60 Degrees X Sqrt 3 Quora
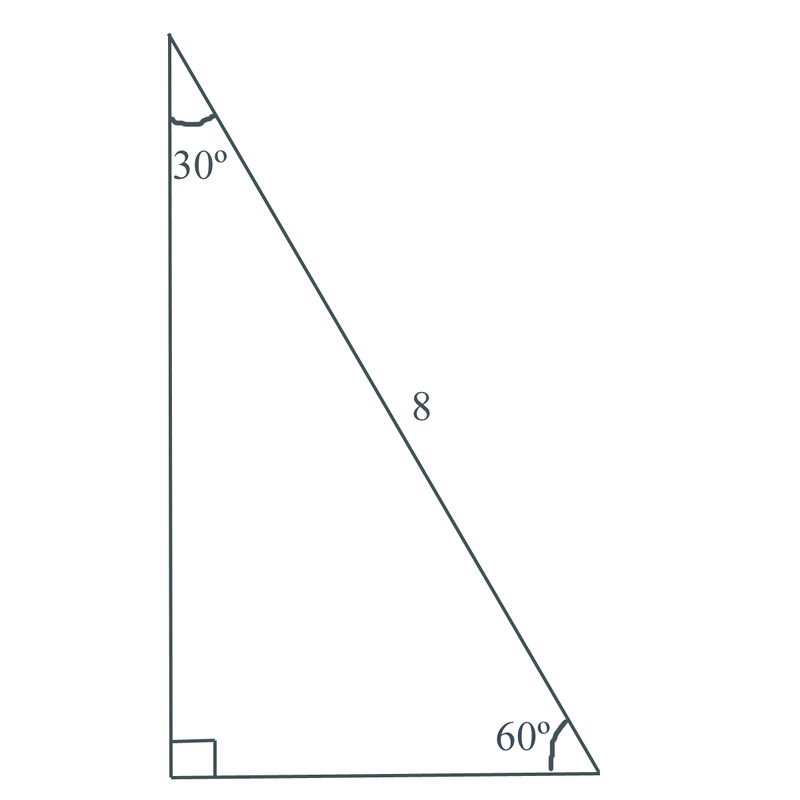
Which is what we set out to prove Corollary The square drawn on the height of an equalateral triangle is three fourths of the square drawn on the sideThis is a triangle with one side length given Let's find the length of the other two sides, a and b Since the side you are given, 8, is across from the 30 degree angle, it will be theThis allows us to find the ratio between each side of the triangle by using the Pythagorean theorem




Special Right Triangles 30 60 90 And 45 45 90 Triangles Youtube




How To Work With 30 60 90 Degree Triangles Education Is Around
Check out this tutorial to learn about triangles!




30 60 90 Triangle Formulas Rules And Sides Science Trends




30 60 90 Right Triangles Free Math Help




Special Right Triangles Video Lessons Examples And Solutions
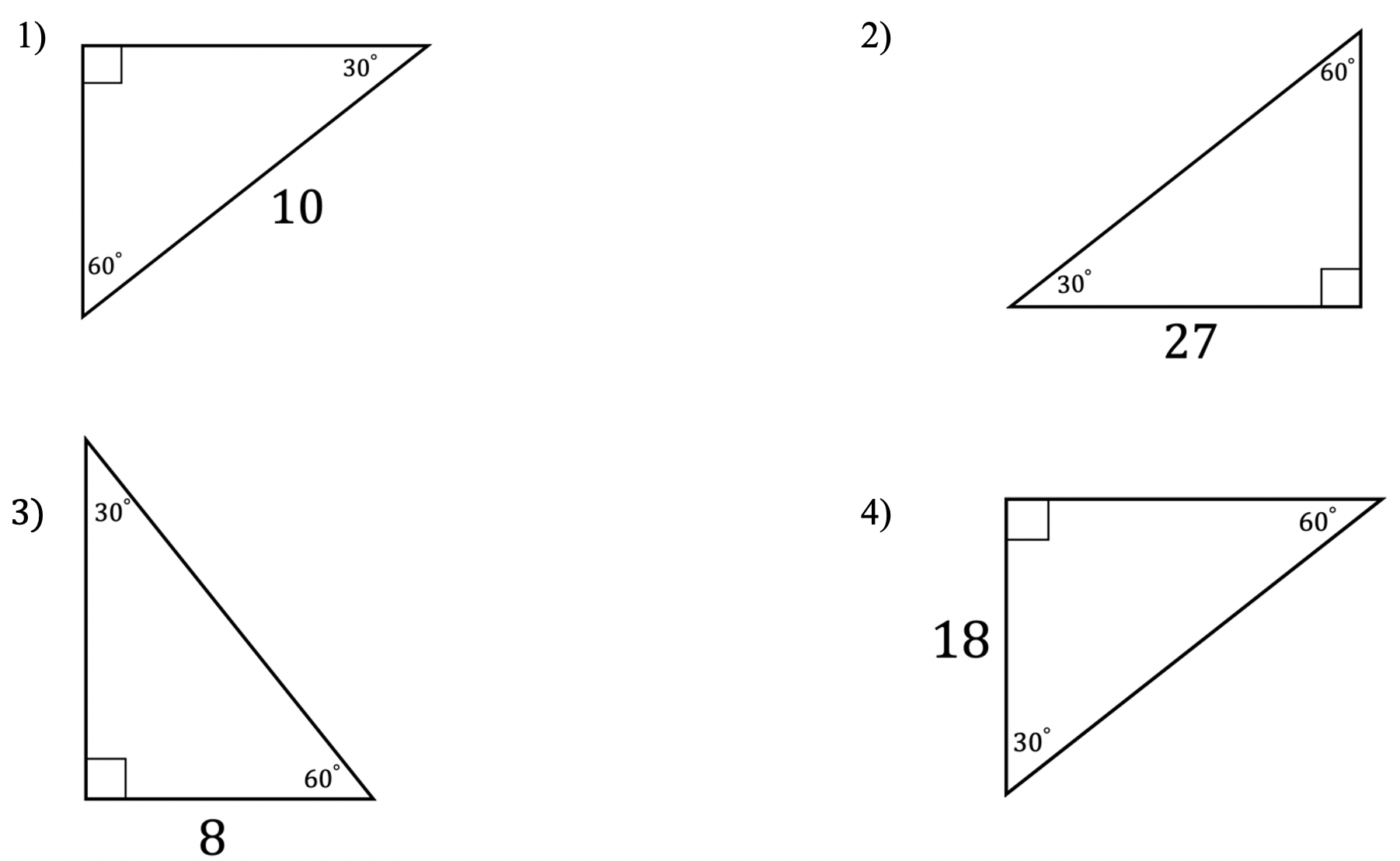



30 60 90 Special Triangles Geometry Mathsux 2




30 60 90 Triangle Explanation Examples




Lesson 11 Triangles 30 60 90 Geogebra
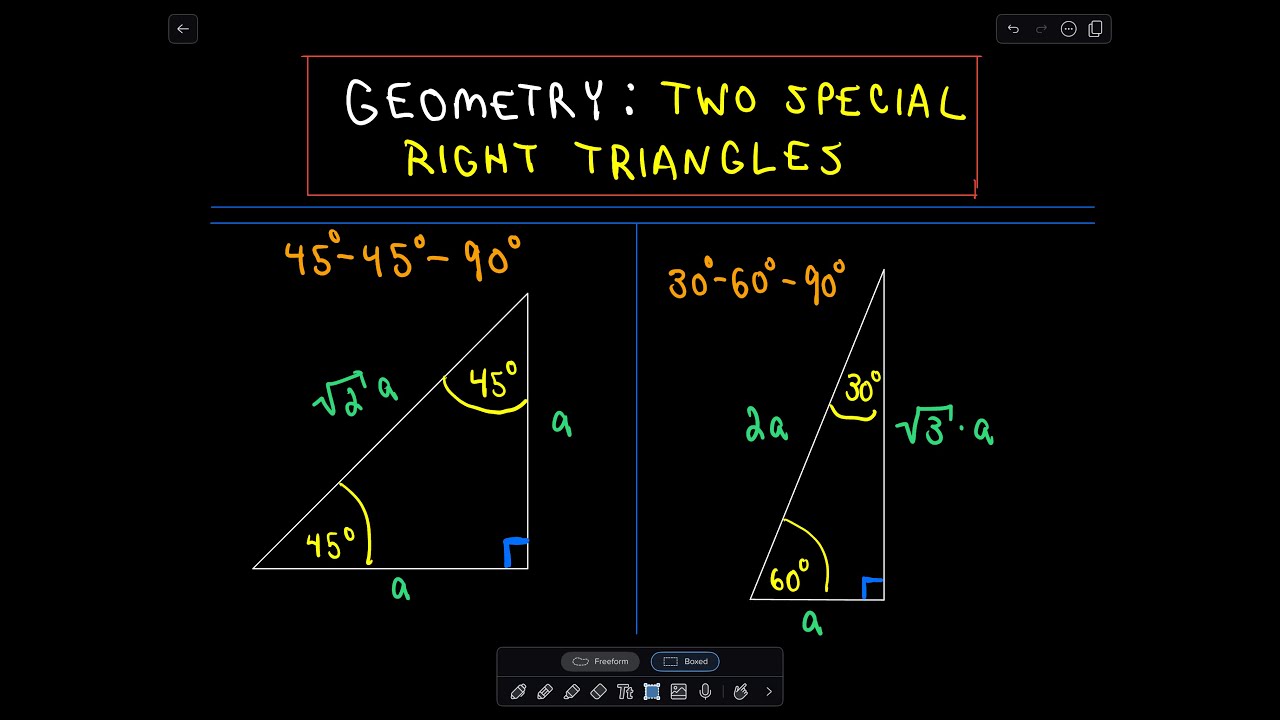



Special Right Triangles In Geometry 45 45 90 And 30 60 90 Youtube




Learn About The 30 60 90 Triangle Caddell Prep Online



30 60 90 Degree Triangle Shefalitayal



Identifying The 30 60 90 Triangles




Special Right Triangles Review Article Khan Academy




How To Use The Special Right Triangle 30 60 90 Studypug




Solved Directions Complete The Following Constructions Chegg Com




Test Prep Thursday Special Right Triangles Mathnasium



45 45 90 And 30 60 90 Triangles Zona Land Education



What Are Some Differences And Similarities Between 30 60 90 Triangles And 45 45 90 Triangle Quora
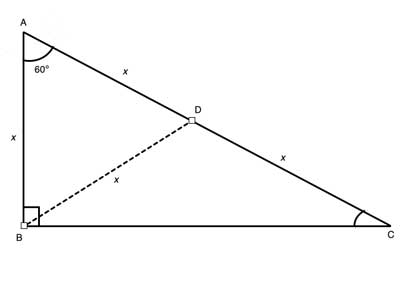



30 60 90 Triangle Geometry Help




Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation
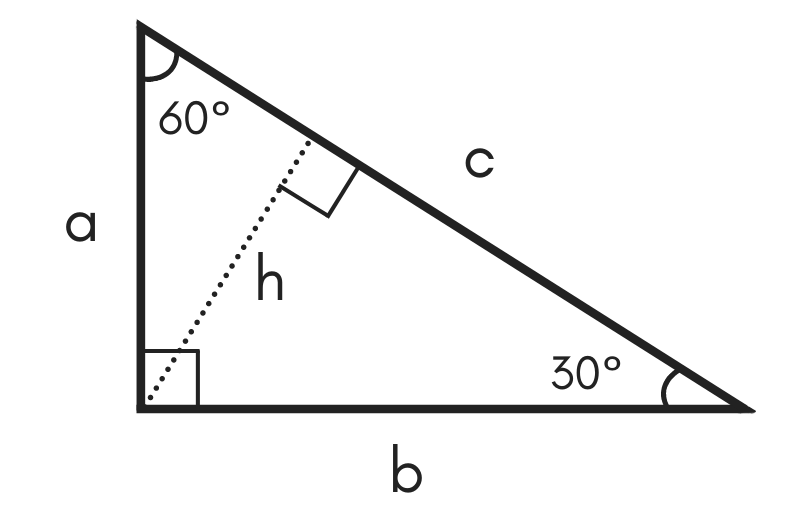



30 60 90 Special Right Triangle Calculator Inch Calculator



A 30 60 90 Triangle Math Central




30 60 90 Triangles



30 60 90 Triangle Formulas Rules And Sides Science Trends




30 60 90 Triangle Theorem Ratio Formula Video



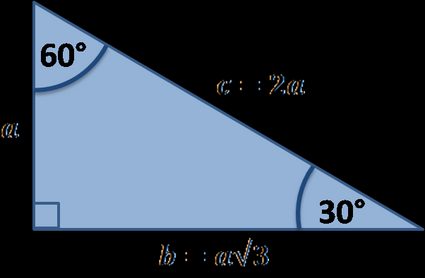
Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation




45 45 90 30 60 90 Mikaelas Dp




30 60 90 Triangle Definition Theorem Formula Examples



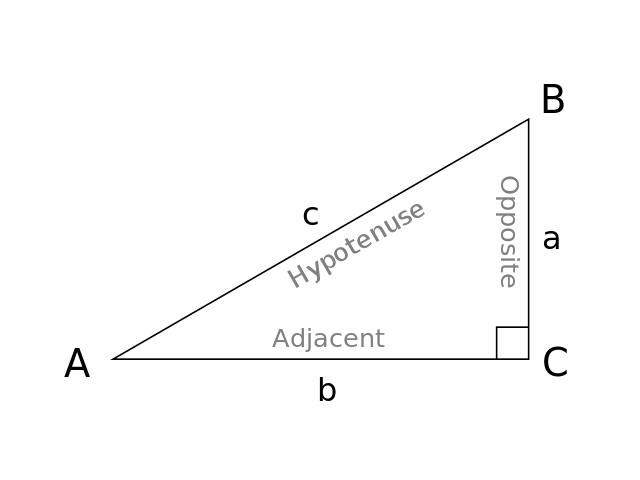
30 60 90 Triangle Calculator Formula Rules




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




Ppt Triangles And Lines Special Right Triangles There Are Two Special Right Triangles Powerpoint Presentation Id




30 60 90 Triangle Theorem Ratio Formula Video



30 60 90 Triangle Formulas Rules And Sides Science Trends




Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math
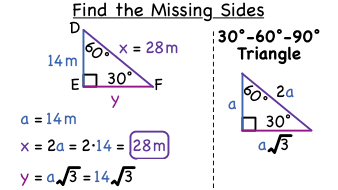



How Do You Find Missing Sides In A 30a 60a 90a Triangle Virtual Nerd



1




How To Construct A 30 60 90 Triangle With Compass And Straightedge Or Ruler Math Open Reference
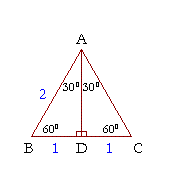



30 60 90 Right Triangle Side Ratios Expii



30 60 90 Triangles Aniya Burroughs
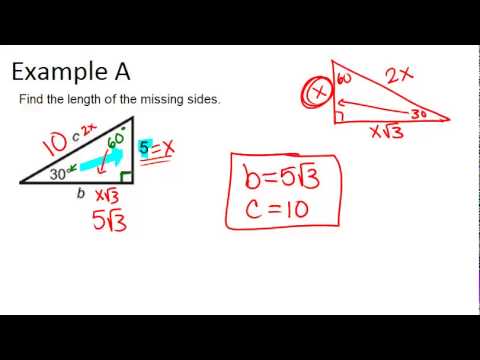



30 60 90 Right Triangles Examples Geometry Concepts Youtube




Special Right Triangles Fully Explained W 19 Examples
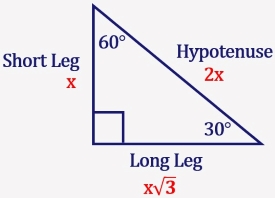



Find The Side Lengths Of A Special Right Triangle 30 60 90 Mathondemand Com




30 60 90 Right Triangles Solutions Examples Videos
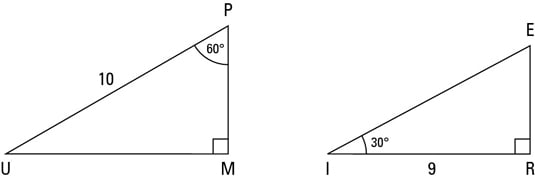



Identifying The 30 60 90 Degree Triangle Dummies



30 60 90 Triangle Definition Theorem Formula Examples
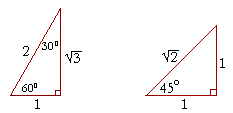



The 30 60 90 Triangle Topics In Trigonometry




A Quick Guide To The 30 60 90 Degree Triangle Dummies



Right Triangle Trigonometry Section 6 5 Pythagorean Theorem




Triangle Gma Is 30 Degree 60 Degree 90 Degree If M 26 Cm Find A And S Study Com



Special Right Triangle 30 60 45 45 37 53 Elearning



30 60 90 Right Triangle How Do I Solve If The Long Leg Is 10 Socratic




30 60 90 Right Triangle Side Ratios Expii




30 60 90 Triangle Theorem Ratio Formula Video




Which Triangle Is A 30 60 90 Triangle Help Brainly Com
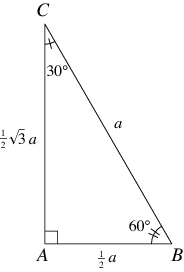



30 60 90 Triangle From Wolfram Mathworld




30 60 90 Triangle Theorem Ratio Formula Video




The Complete Guide To The 30 60 90 Triangle
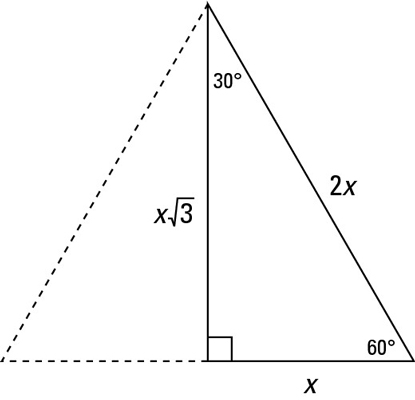



Identifying The 30 60 90 Degree Triangle Dummies
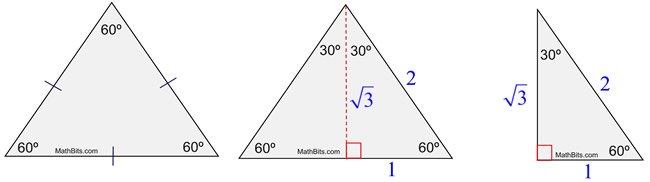



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math




30 60 90 Triangle Example Problem Video Khan Academy
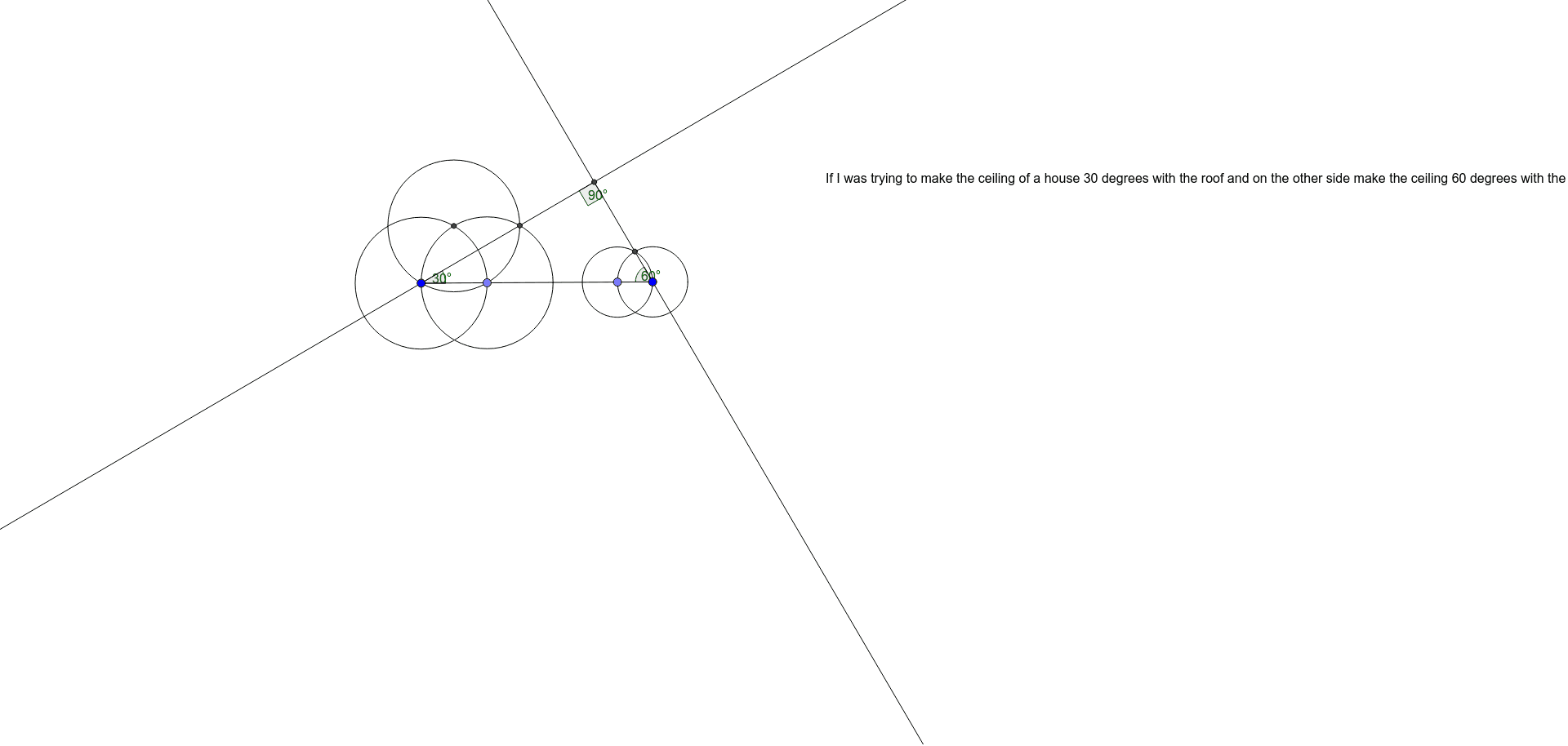



How To Construct A 30 60 90 Degree Triangle Geogebra




Special Right Triangle Wikipedia
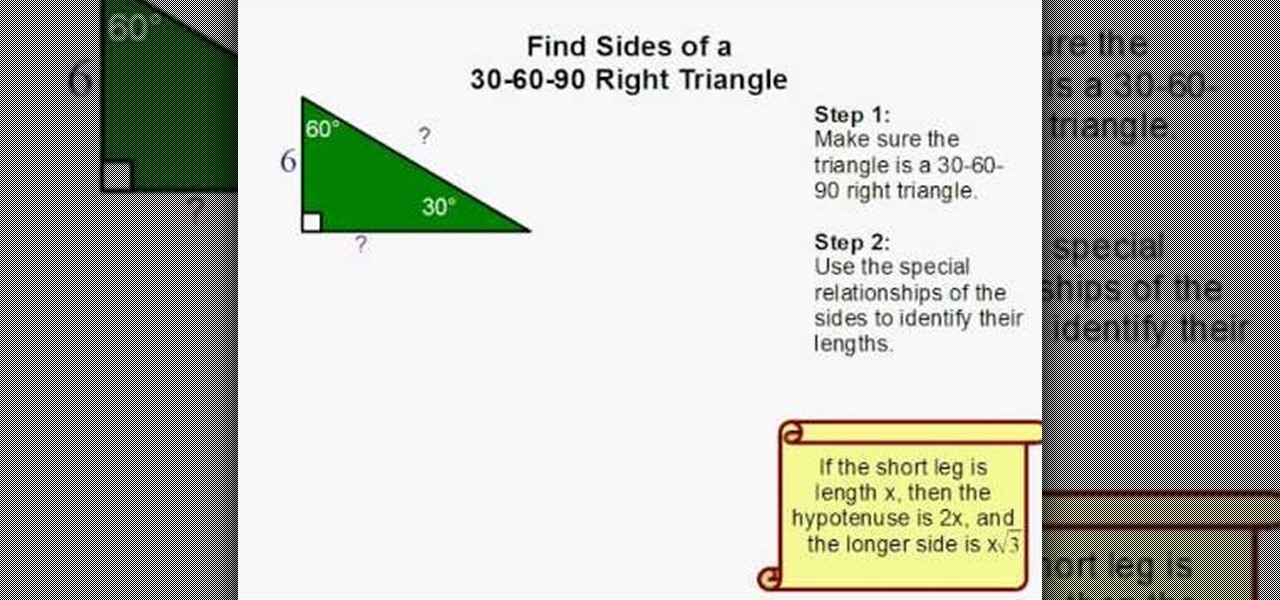



How To Find The Sides Of A 30 60 90 Right Triangle Math Wonderhowto




Solved Directions Complete The Following Constructions Chegg Com



Tools Workshop Equipment Set Of 2 Eboot Large Triangle Ruler Square Set 30 60 And 45 90 Degrees Measuring Layout Tools



Solve A 30 60 90 Triangle With Gradea




30 60 90 Triangle Calculator Formula Rules



A 30 60 90 Triangle



Trigonometry



The Easy Guide To The 30 60 90 Triangle




The 30 60 90 Triangle Topics In Trigonometry




A Quick Guide To The 30 60 90 Degree Triangle Dummies




The 30 60 90 Triangle Topics In Trigonometry




30 60 90 Triangle Explanation Examples



Solve A 30 60 90 Triangle With Gradea




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Definition Theorem Formula Examples




The Complete Guide To The 30 60 90 Triangle



The Easy Guide To The 30 60 90 Triangle




Which 30 60 90 Degree Triangle Is Labeled With The Correct Side Length Ratio Brainly Com


